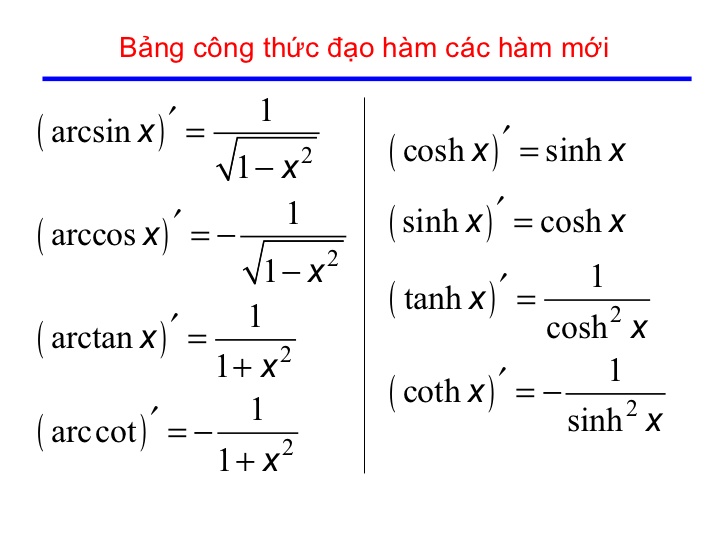
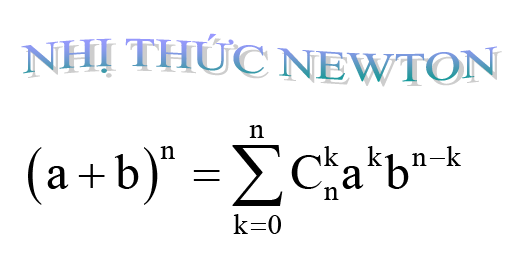Bài 3: Đạo hàm của hàm số lượng giác (Giải bài tập 7,8)
Bài 7. (Hướng dẫn giải trang 169 sgk Giải tích 11 cơ bản)
Giải phương trình f'(x) = 0, biết rằng:
a) f(x) = 3cosx + 4sinx + 5x;
b) f(x) = 1 – sin(π + x) + 2cos(2π+x)/2
Hướng dẫn giải:
a) f'(x) = – 3sinx + 4cosx + 5. Do đó
f'(x) = 0 <=> – 3sinx + 4cosx + 5 = 0 <=> 3sinx – 4cosx = 5
<=> 3/5sinx – 4/5cosx = 1. (1)
Đặt cos φ = 3/5, (φ ∈ (0;π/2) => sin φ = 4/5
Ta có:
(1) <=> sinx.cos φ – cosx.sin φ = 1 <=> sin(x – φ) = 1
Tài liệu học tập lớp 6
Tài liệu học tập lớp 7
Tài liệu học tập lớp 8
Tài liệu học tập lớp 9
Tài liệu học tập lớp 10
Tài liệu học tập lớp 11
Tài liệu học tập lớp 12
Kiến thức cơ bản
Tài liệu học tập lớp 7
Tài liệu học tập lớp 8
Tài liệu học tập lớp 9
Tài liệu học tập lớp 10
Tài liệu học tập lớp 11
Tài liệu học tập lớp 12
Kiến thức cơ bản
Bài 3: Đạo hàm của hàm số lượng giác (Giải bài tập 7, 8) , ,
Cho chúng tôi biết ý kiến của bạn?
Đắm mình trong hối tiếc là tiêu phí thời giờ hôm nay cho thời giờ đã qua không thuộc về chúng ta nữa.
Khuyết danh
Quan Tâm ?
Bài 3: Cấp số cộng (Giải bài tập 4,5)Bài 5: Đạo hàm cấp hai (Giải bài tập 1,2)Bài 4: Phép thử và biến cố (Giải bài tập 4,5)Bài 3: Cấp số cộng (Giải bài tập 1,2,3)Bài 5: Xác xuất của biến cố (Giải bài tập 1,2,3)Bài 3: Đạo hàm của hàm số lượng giác (Giải bài tập 4,5,6)Bài 3: Hàm số liên tục (Giải bài tập 4,5,6)
Ngẫu Nhiên
Chứng minh cuộc đời và thơ văn của Nguyễn Trãi thể hiện được tinh thần, tư tưởng trong bài “Bình ngô đại cáo”Bài 34: Vitamin Và Muối KhoángBài 2: Dân số và gia tăng dân sốBài 4: Sóng điện từ (Giải bài tập 1, 2, 3, 4, 5, 6)Reading Unit 4 Lớp 11 Trang 46Bài 22: Nhân dân hai miền trực tiếp chiến đấu chống đế quốc Mĩ xâm lược. Nhân dân miền Bắc vừa chiến đấu vừa sản xuất (1965-1973)Bài 7: Bài tập chương IBài 47: Châu Nam Cực - châu lục lạnh nhất thế giới